How Functional Isolation Forest Detects Anomalies

Table of Links

Abstract and 1. Introduction

2. Background & Preliminaries

2.1. Functional Isolation Forest

2.2. The Signature Method

3. Signature Isolation Forest Method

4. Numerical Experiments

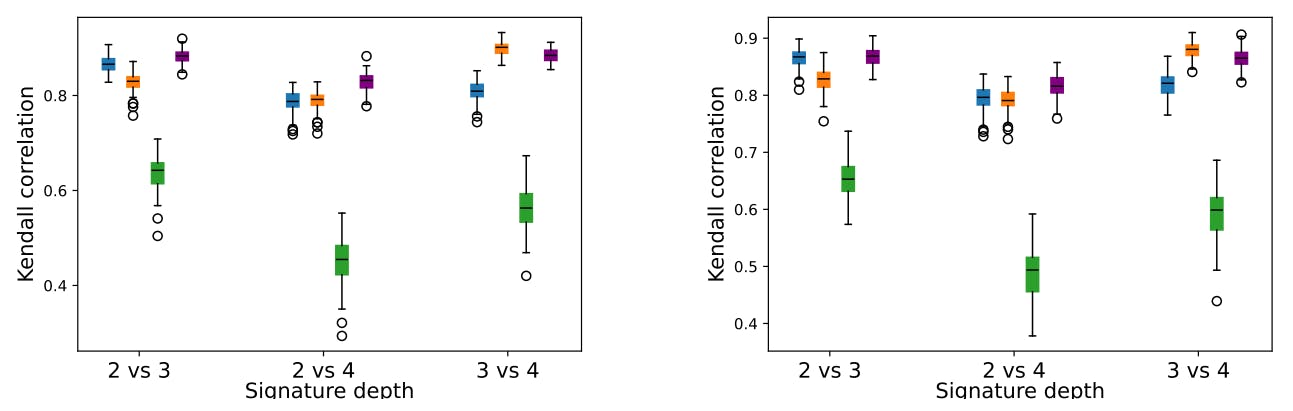
4.1. Parameters Sensitivity Analysis

4.2. Advantages of (K-)SIF over FIF

4.3. Real-data Anomaly Detection Benchmark

5. Discussion & Conclusion, Impact Statements, and References

Appendix

A. Additional Information About the Signature

B. K-SIF and SIF Algorithms

C. Additional Numerical Experiments

2. Background & Preliminaries

2.1. Functional Isolation Forest

Consider H the functional Hilbert space equipped with a inner product ⟨., .⟩H such that any x ∈ H is a real function defined on [0, 1]. A Functional Isolation Forest is created through an assembly of functional isolation trees (F-itrees). Each F-itree is constructed via a series of random splits from a subsample (of size m) of Xn. The abnormality score for an observation x is then determined as a monotonically decreasing transformation of x’s average depth across the trees. The core concept lies in the randomness of the splits, where an observation markedly different from others is more likely to be isolated from Xn, appearing at shallower levels in the F-itrees. The F-itrees are built based on a predetermined dictionary D ⊂ H, encompassing both deterministic and/or stochastic functions capturing pertinent data properties, which may also be a subset of Xn. Before each random univariate split, all node observations are projected onto a line defined by a randomly selected element from the dictionary D. The selection of a suitable dictionary plays a pivotal role in shaping the FIF score construction. The projection criterion at each node of each F-itree is defined as: