What is the Signature Isolation Forest?

Table of Links

Abstract and 1. Introduction

2. Background & Preliminaries

2.1. Functional Isolation Forest

2.2. The Signature Method

3. Signature Isolation Forest Method

4. Numerical Experiments

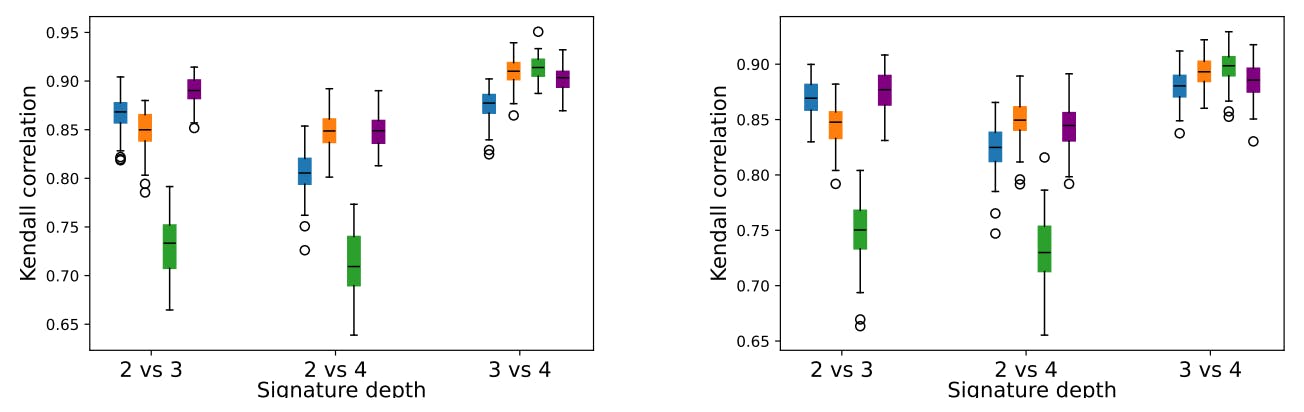
4.1. Parameters Sensitivity Analysis

4.2. Advantages of (K-)SIF over FIF

4.3. Real-data Anomaly Detection Benchmark

5. Discussion & Conclusion, Impact Statements, and References

Appendix

A. Additional Information About the Signature

B. K-SIF and SIF Algorithms

C. Additional Numerical Experiments

Abstract

Functional Isolation Forest (FIF) is a recent stateof-the-art Anomaly Detection (AD) algorithm designed for functional data. It relies on a tree partition procedure where an abnormality score is computed by projecting each curve observation on a drawn dictionary through a linear inner product. Such linear inner product and the dictionary are a priori choices that highly influence the algorithm’s performances and might lead to unreliable results, particularly with complex datasets. This work addresses these challenges by introducing Signature Isolation Forest, a novel AD algorithm class leveraging the rough path theory’s signature transform. Our objective is to remove the constraints imposed by FIF through the proposition of two algorithms which specifically target the linearity of the FIF inner product and the choice of the dictionary. We provide several numerical experiments, including a real-world applications benchmark showing the relevance of our methods.

1. Introduction

The development of sophisticated anomaly detection (AD) methods plays a central role in many areas of statistical machine learning, see Chandola et al. (2009). The area of AD is growing increasingly complex, especially in large data applications such as in network science or functional data analysis.

In the classical AD multivariate scenario, observations can be represented as points in R d and various methodologies have been introduced in the literature. A model-based approach is favored when there is knowledge about the datagenerating process (Rousseeuw and Driessen, 1999). Conversely, in numerous real-world applications where the underlying data system is unknown, nonparametric approaches 1 INRIA, CEA, Univ. Paris-Saclay, France. 2CERIAH, Institut de l’Audition, Institut Pasteur, France. 3Department of Statistics & Applied Probability, University of California Santa Barbara, USA. Correspondence to: Guillaume Staerman . are preferred (Polonik, 1997; Scholkopf et al., 2001).

The area of AD is only just beginning to explore the domain of functional data. Functional data is becoming an important discipline in topological data analysis and data science, see Ramsay and Silverman (2005); Ferraty (2006) or Wang et al. (2016) for more details. In essence, functional data involves treating observations as entire functions, curves, or paths. In some application domains, this approach can provide richer information than just a sequence of data observation vectors, yet it comes with challenges, especially when considering the development of AD methods.

In the use of AD within a functional data context, the anomaly detection task involves identifying which functions/curves differ significantly in the data to be considered anomalous in some sense. Following Hubert et al. (2015), three types of basic anomalies can be detected: shift, shape, amplitude. These anomalies can then be isolated/transient or persistent depending on the frequency of their occurrences. Some are easier/more difficult to identify than others, e.g. an isolated anomaly in shape is much more complex than a persistent anomaly in amplitude.

At first sight, one may adopt a preliminary filtering technique. This leads to projecting the functional data onto a suitable finite-dimensional function subspace. It can be done by projecting onto a predefined basis such as Fourier or Wavelets or on a data-dependent Karhunen-Loeve basis by means of Functional Principal Component Analysis (FPCA; Dauxois et al., 1982; Shang, 2014). The coefficients describing this subspace are then used as input into a specific anomaly detection (AD) algorithm designed for multivariate data.

In this approach, the a priori choice of basis to undertake the projection can significantly influence the ability to detect particular types of anomalies in the functional data accurately. This makes these approaches sensitive to such choices. In other words, the choice of a given bases for projection can artificially amplify specific patterns or make others disappear entirely, depending on their properties. Therefore, it is a choice highly sensitive to the knowledge of the underlying studied process, which is a must for such an AD method to work.

If one seeks to avoid this projection methods that take functional data to a parameter vector space to undertake the AD method, one may alternatively seek AD methods working directly in the function space. This is the case of functional data depth, which takes as input a curve and a dataset of curves and returns a score indicating how deep the curve w.r.t. the dataset is. Many functional data depths, with different formulations, have been designed so far, such as, among others, the functional Tukey depth (Fraiman and Muniz, 2001; Claeskens et al., 2014), the Functional StahelDonoho Outlyingness (Hubert et al., 2015), the ACH depth (Staerman et al., 2020), the band depth (Lopez-Pintado and ´ Romo, 2009) or the half-region depth (Lopez-Pintado and ´ Romo, 2011); see Nieto-Reyes and Battey (2016); Gijbels and Nagy (2017) or the Chapter 3 of Staerman (2022) for a detailed review of functional depths.

One may also extend the classical anomaly detection algorithms designed for multivariate data such as the one-class SVM (OCSVM; Scholkopf et al. ¨ , 2001), Local Outlier Factor (LOF; Breunig et al., 2000) or Isolation Forest (IF; Liu et al., 2008) to the functional setting, see Rossi and Villa (2006). Recently, Staerman et al. (2019) introduced a novel algorithm, Functional Isolation Forest (FIF), which extends the popular IF to an infinite-dimensional case. It faces the challenge of adaptively (randomly) partitioning the functional space to separate trajectories in an iterative partition. Based on the computational advantages of random treebased structures and their flexibility in choosing the split criterion related to functional properties of the data, it has been considered a powerful and promising approach for functional anomaly detection (Staerman et al., 2023).

Although FIF offers a robust solution for functional data, three main challenges arise when it is applied in practice. Firstly, the selection of two critical parameters involved in the splitting criterion: the functional inner product and the dictionary of time-frequency atoms for data representation. The choice of these elements significantly influences the algorithm’s performance, potentially compromising its flexibility. Secondly, the splitting criterion is formulated as a linear transformation of the dictionary function and a sample curve, potentially constrained in capturing more complex data, including non-stationary processes. Thirdly, when dealing with multivariate functions, FIF takes into account dimension dependency only linearly by using the sum of the inner product of each marginal as a multivariate inner product and may not capture complex interactions of the multivariate process. It is crucial to address these challenges to enhance the overall efficacy and adaptability of the FIF algorithm in practical applications.

In response to the above challenges, we propose a new class of algorithms, named (KERNEL-) SIGNATURE ISOLATION FOREST, by leveraging the signature technique derived from rough path theory (Lyons et al., 2007; Friz and Victoir, 2010). In rough path theory, functions are usually referred to as paths to characterize their geometrical properties. The signature transform, or signature of a path, summarizes the temporal (or sequential) information of the paths. In practice, it captures the sequencing of events and the path’s visitation order to locations. Yet, it entirely disregards the parameterization of the data, providing flexibility regarding the partial observation points of the underlying functions/paths. Consider a path in a multidimensional space of dimension d, i.e. x ∈ Fd , where the path consists of a sequence of data points. The signature of this path is a collection of iterated integrals of the path with respect to time. By including these iterated integrals up to a certain level, the signature provides a concise and informative representation of the path, allowing for extracting meaningful features. This makes it particularly useful in analyzing sequential data, such as time series. The idea behind such a transform is to produce a feature summary of the data system, which captures the main events of the data and the order in which they happen, without recording when they occur precisely (Lyons and McLeod, 2022). Performances of signature-based approaches appear to be promising, as they achieve state-of-the-art in some applications such as handwriting recognition (Wilson-Nunn et al., 2018; Yang et al., 2016b), action recognition (Yang et al., 2016a), and medical time series prediction tasks (Morrill et al., 2019). Surprisingly, it has been overlooked in the Machine Learning problems and has never been used in functional anomaly detection until we make this novel connection.

Our idea is to perform anomaly detection by isolating multivariate functions corresponding to sets of paths subject to the signature transform. Hence, the tree partitioning of FIF will now take place on the feature space of the signature transform. In such a way, the functional data changes are captured by embedding the studied data set into a path whose changes are then summarized by the signature method. We propose two different algorithms named KERNEL SIGNATURE ISOLATION FOREST (K-SIF) and SIGNATURE ISOLATION FOREST (SIF). The first algorithm extends the FIF procedure to nonlinear transformations by using the signature kernel instead of the inner product of FIF. Relying on the attractive properties of the signature, see Fermanian (2021); Lyons and McLeod (2022) or Section 2.2, our algorithms take into account higher moments of the functions (derivative, second-order derivative, etc.) hence accommodating changes (or oscillations) of different nature. The second algorithm is a more straightforward procedure relying on what is usually referred to as ‘coordinate signature’, defined in Section 2, and being free of any sensitive parameters such as the dictionary (for FIF and K-SIF) and the inner product (for FIF). It removes the performance variability of the parameters used in FIF.

• We introduce two functional anomaly detection algorithms (K-SIF and SIF) based on the isolation forest structure and the signature approach from rough path theory.

• The two algorithms provide improvements in the functional anomaly detection community by extending Functional Isolation Forest in two directions: the first one considers non-linear properties of the underlying data, hence providing a more suitable procedure for a more challenging dataset; the second one is an entirely data-driven technique free from any a priori choice due to a dictionary selection constraining the functional AD procedure to identify only specific types of patterns.

• After studying the behavior of our class of algorithm regarding their parameters, we highlight the benefits of using (K-)SIF over FIF. On a competitive benchmark, we show that K-SIF, which extends the FIF procedure through the signature kernel, consistently showed the results of FIF on real-world datasets. Furthermore, we show that SIF achieves state-of-the-art performances while being more consistent than FIF.