Authors:
(1) Guillaume Staerman, INRIA, CEA, Univ. Paris-Saclay, France;
(2) Marta Campi, CERIAH, Institut de l’Audition, Institut Pasteur, France;
(3) Gareth W. Peters, Department of Statistics & Applied Probability, University of California Santa Barbara, USA.
Table of Links
2.1. Functional Isolation Forest
3. Signature Isolation Forest Method
4.1. Parameters Sensitivity Analysis
4.2. Advantages of (K-)SIF over FIF
4.3. Real-data Anomaly Detection Benchmark
5. Discussion & Conclusion, Impact Statements, and References
Appendix
A. Additional Information About the Signature
C. Additional Numerical Experiments
2.2. The Signature Method
The signature of a path is a sequence of iterated integrals that captures important information about the path’s geometric and topological features (Lyons et al., 2007; Fermanian, 2021).
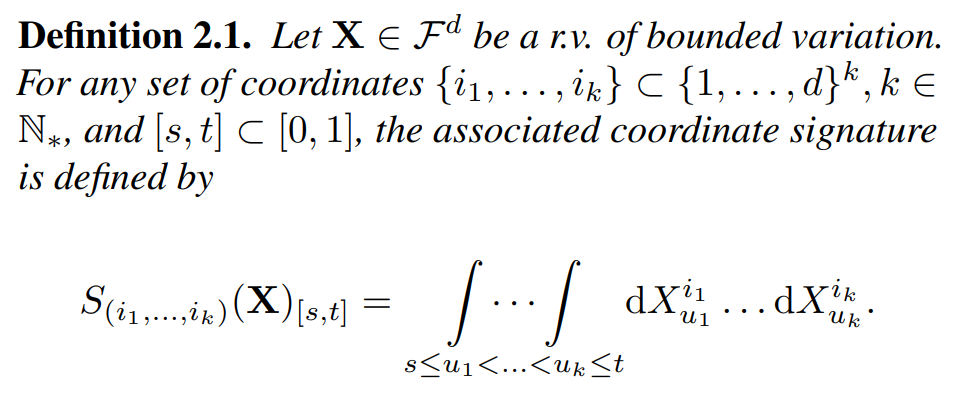
Furthermore, the signature of X is defined as the infinite collection of coordinate signature
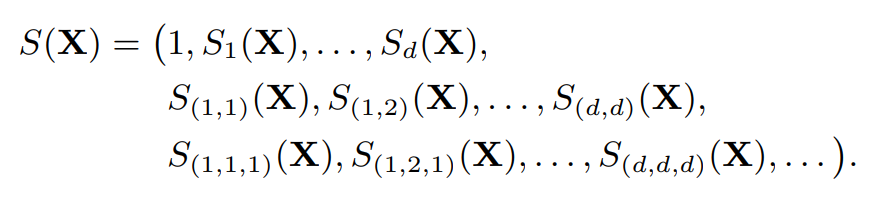


One may refer to Lee and Oberhauser (2023) for an account of the untruncated kernel signature. See also Section A in the Appendix for further details about the signature and its properties.
This paper is available on arxiv under CC BY 4.0 DEED license.