Authors:
(1) Guillaume Staerman, INRIA, CEA, Univ. Paris-Saclay, France;
(2) Marta Campi, CERIAH, Institut de l’Audition, Institut Pasteur, France;
(3) Gareth W. Peters, Department of Statistics & Applied Probability, University of California Santa Barbara, USA.
Table of Links
2.1. Functional Isolation Forest
3. Signature Isolation Forest Method
4.1. Parameters Sensitivity Analysis
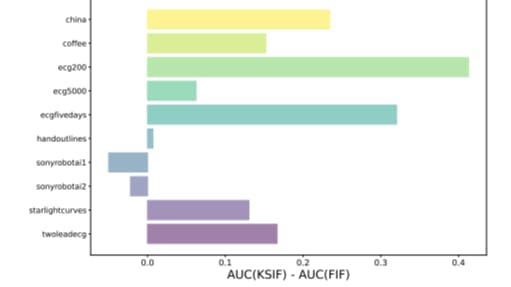
4.2. Advantages of (K-)SIF over FIF
4.3. Real-data Anomaly Detection Benchmark
5. Discussion & Conclusion, Impact Statements, and References
Appendix
A. Additional Information About the Signature
C. Additional Numerical Experiments
A. Additional Information About the Signature
In this section, we provide additional information regarding the signature. Firstly, the formula for the coordinate signature is provided, followed by some further information about the truncated signature and the link of the signature with moments. We then introduce references and further discussion for the computation of the signature, the linear-closed form utilised and, lastly, a review of the inner product of tensors required for the signature method is presented.

Computation of the Signature. The signature is usually computed on the linear paths reconstructed from observations (Lyons and McLeod, 2022; Fermanian, 2021) thanks to the two properties listed below. First, the signature benefits from a closed form when computed on linear paths. Second, a concatenation formula has been provided by Chen (1958), where the coordinate signature of two concatenate segments is given by a tensor product of the specific coordinate signatures on each segment. These two properties are described formally below.

In practice, the signature is usually computed as follows. First, a linear path is reconstructed by interpolation from the observed data. In a second step, the signature of each segment of the linear path are calculated separately thanks to the closed-form (2). Then the signature of the entire path is computed recursively using the Chen’s identity property.

Definition of Inner Product of Tensors for Signature Method. Following Chevyrev and Oberhauser (2022) and Lee and Oberhauser (2023), we introduce the inner product of the tensors required to compute the truncated signature and its kernel.

This paper is available on arxiv under CC BY 4.0 DEED license.