Authors:
(1) Haleh Hayati, Department of Mechanical Engineering, Dynamics and Control Group, Eindhoven University of Technology, The Netherlands;
(2) Nathan van de Wouw, Department of Mechanical Engineering, Dynamics and Control Group, Eindhoven University of Technology, The Netherlands;
(3) Carlos Murguia, Department of Mechanical Engineering, Dynamics and Control Group, Eindhoven University of Technology, The Netherlands, and with the School of Electrical Engineering and Robotics, Queensland University of Technology, Brisbane, Australia.
Table of Links
General Guidelines for Implementation
II. PROBLEM FORMULATION
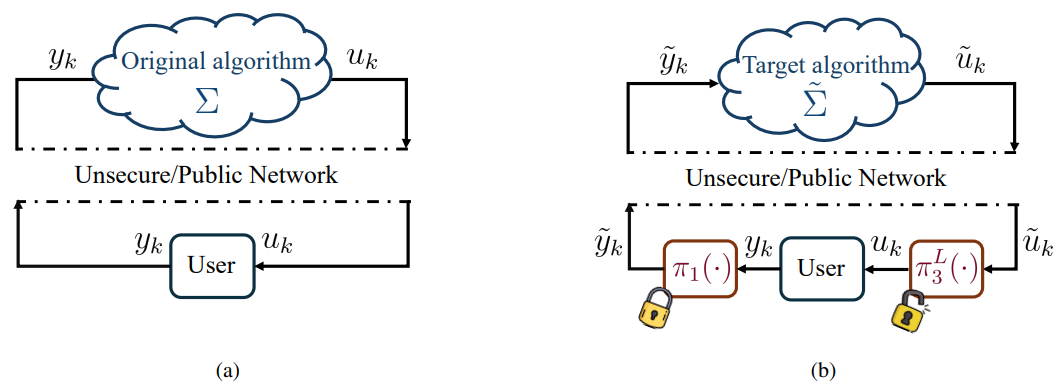
The setting that we consider is the following. The user aims to run an algorithm remotely (in the cloud) using her/his local data yk to produce some data utility uk (what the algorithm returns), see Fig. 1(a). However, the user does not want to share the original data yk as it contains sensitive private information that could be inferred. The goal of our proposed privacy-preserving scheme is to devise an encoding mechanism to mask the original data and the algorithm to be run in the cloud so that inference of sensitive information from the encoded disclosed data is as hard as possible (in a probabilistic Differential-Privacy (DP) sense) without degrading the performance of the encoded algorithm (so a homomorphic probabilistic scheme).






A. Immersion-based Coding



We now have all the ingredients to pose the problem we seek to address.

The flowchart of the original algorithm and the target algorithm are shown in Fig. 1.
Remark 1 Note that solutions to Problem 1 characterize a class of encoding maps and target algorithms for which we can design homomorphic encryption schemes (a prescriptive design, i.e., for given (f, g, ζ0)) that operate over the reals. However, this class is infinite-dimensional (over a function space). It leads to an underdetermined algebraic problem with an infinite dimensional solution space. To address this aspect of the problem, we impose structure on the maps we seek to design. We restrict to random affine maps composed of linear coordinate transformations and additive random processes. In what follows, we prove that this class of maps is sufficient to guarantee an arbitrary level of differential privacy.
This paper is available on arxiv under CC BY 4.0 DEED license.

