Authors:
(1) Haleh Hayati, Department of Mechanical Engineering, Dynamics and Control Group, Eindhoven University of Technology, The Netherlands;
(2) Nathan van de Wouw, Department of Mechanical Engineering, Dynamics and Control Group, Eindhoven University of Technology, The Netherlands;
(3) Carlos Murguia, Department of Mechanical Engineering, Dynamics and Control Group, Eindhoven University of Technology, The Netherlands, and with the School of Electrical Engineering and Robotics, Queensland University of Technology, Brisbane, Australia.
Table of Links
General Guidelines for Implementation
III. AFFINE SOLUTION TO PROBLEM 1
In this section, we construct a prescriptive solution to Problem 1 using random affine maps. Let the user data encoding map π1(·), the immersion map π2(·), and the utility map π3(·) be affine functions of the form:




We can now state the proposed solution to Problem 1

Proof: Proposition 1 follows from the discussion provided in the solution section above, Section II
Remark 2 In Proposition 1, we present the first part of the design of the proposed immersion-based coding mechanism for privacy. Note that the proposed scheme is independent of the nature of the user data yk and utility uk, and does not require any assumption on the original algorithm. These features make the proposed scheme suitable to enforce privacy for a large class of linear and nonlinear high-dimensional algorithms.
Remark 3 This manuscript primarily focuses on immersionbased coding for privacy of discrete-time algorithms operating in the cloud. It is noteworthy that it can be proved that the application of the proposed coding and target algorithm in Proposition 1 can be extended for privacy of continuous-time systems. This extension highlights the wider application of the immersion-based coding, providing a solution for cloud-based privacy covering discrete and continuous-time algorithms.
A. Algorithms with Different Time-Scale
The class of algorithms considered in (1), and the results that followed, operates on a single time scale. That is, the algorithm reacts to the received yk, iterates once according to f(·) and g(·), and sends the utility uk back to the user. This is repeated sequentially between the user and the cloud. Algorithms that fit this class are, e.g., control, monitoring, and federated learning schemes. Note, however, that there are many algorithms that operate on a different time scale from that of the user. That is, there are algorithms that receive the user data yk at time k, iterate locally multiple times in the cloud (say for t = 1, . . . , T), and only after a number of local iterations (T), the data utility uk is sent back to the user. Algorithms that fit this class are, for instance, general learning algorithms where it is often the case that the complete data set is uploaded to the cloud, the training is done there by running gradient-like steps multiple times, and only when the cost function has decreased to an acceptable level, the final trained model is sent back to the use
For the sake of completeness, we concisely provide the corresponding coding result for algorithms with different time scales. Consider discrete-time dynamic algorithms of the for

Further, consider the corresponding higher-dimensional target algorithm:

Following the reasoning described in the above section, for algorithm (19) and corresponding target algorithm (20), we let the user data encoding map, the immersion map, and the utility map be affine functions of the form:
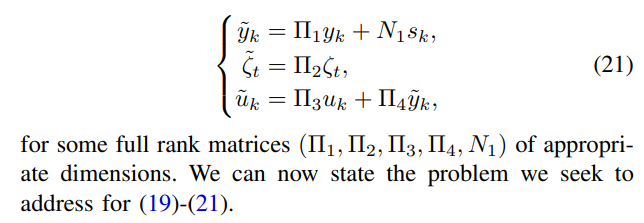

Problem 2 is an analogue to Problem 1 for systems with two time scales. Following the lines of the solution to Problem 1, we provide a solution to Problem 2 in the following corollary of Proposition 1.

Proof: The proof of Corollary 1 follows the same lines as the proof of Proposition 1. Only the time scales of the encoded signals change. The proof is omitted here for the sake of brevity.
So far, we have presented the proposed immersion-based coding for two classes of discrete-time algorithms built around stochastic affine maps. Note that the only constraint on these maps is that they are full-rank. In the next section, we state sufficient conditions for the proposed privacy scheme to guarantee a prescribed level of differential privacy.
This paper is available on arxiv under CC BY 4.0 DEED license.

