Authors:
(1) Junwei Su, Department of Computer Science, the University of Hong Kong and [email protected];
(2) Chuan Wu, Department of Computer Science, the University of Hong Kong and [email protected].
Table of Links
5 A Case Study on Shortest-Path Distance
6 Conclusion and Discussion, and References
9 Procedure for Solving Eq. (6)
10 Additional Experiments Details and Results
11 Other Potential Applications
6 Conclusion and Discussion
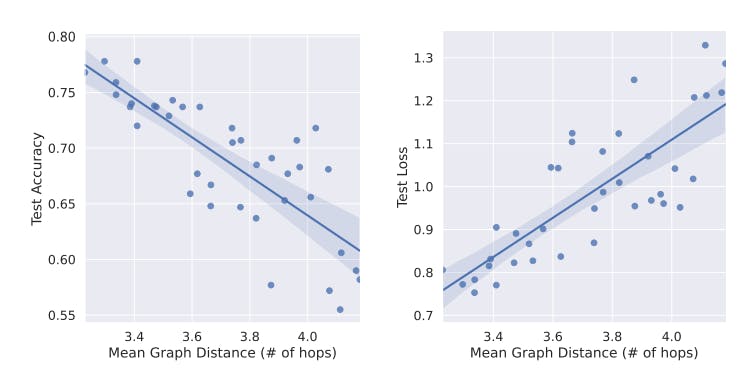
In this work, we study and investigate GNNs which are fundamental to many computer vision and machine learning tasks. In particular, we explore the relationship between the topology awareness and generalization performance of GNNs. We introduce a novel framework that connects the structural awareness of GNNs with approximate metric embedding, offering a fresh perspective on their generalization capabilities in semi-supervised node classification tasks. This structure-agnostic framework facilitates a deeper, more intuitive comprehension of GNN generalizability across varied graph structures. Through a case study centered on graph distance, we demonstrate that our theoretical findings regarding structural results are reflected in the practical generalization performance of GNNs. Additionally, our findings shed light on the cold start problem in graph active learning and could influence various significant GNN applications.
6.1 Limitation and Future Works
Our proposed framework introduces a novel angle on GNN generalization performance, yet it is not without limitations. The current approach interprets GNN embeddings in terms of metric mapping and describes the structure awareness of GNNs through distortion. This perspective, however, overlooks the specific dynamics that contribute to reduced distortion within GNNs. Investigating these underlying dynamics would significantly enrich this area of research. Moreover, our study primarily examines the transductive setting. Expanding this analysis to the inductive setting—where the model is trained on one graph but applied to another—would offer a more comprehensive view of GNN generalization capabilities.
References
-
Ali, J., Babaei, M., Chakraborty, A., Mirzasoleiman, B., Gummadi, K.P., Singla, A.: On the fairness of time-critical influence maximization in social networks. In: 2022 IEEE 38th International Conference on Data Engineering (ICDE). pp. 1541–IEEE (2022)
-
Balestriero, R., richard baraniuk: A spline theory of deep learning. In: Dy, J., Krause, A. (eds.) Proceedings of the 35th International Conference on Machine Learning. Proceedings of Machine Learning Research, vol. 80, pp. 374–383. PMLR (10–15 Jul 2018), https://proceedings.mlr.press/v80/balestriero18b.html
-
Baranwal, A., Fountoulakis, K., Jagannath, A.: Graph convolution for semisupervised classification: Improved linear separability and out-of-distribution generalization. arXiv preprint arXiv:2102.06966 (2021)
-
Bojchevski, A., Günnemann, S.: Deep gaussian embedding of graphs: Unsupervised inductive learning via ranking (2018)
-
Cai, H., Zheng, V.W., Chang, K.C.C.: Active learning for graph embedding. arXiv preprint arXiv:1705.05085 (2017)
-
Chen, J., Zhu, J., Song, L.: Stochastic training of graph convolutional networks with variance reduction. arXiv preprint arXiv:1710.10568 (2017)
-
Chen, M., Wei, Z., Huang, Z., Ding, B., Li, Y.: Simple and deep graph convolutional networks (2020)
-
Dong, Y., Ma, J., Chen, C., Li, J.: Fairness in graph mining: A survey (2022). https://doi.org/10.48550/ARXIV.2204.09888, https://arxiv.org/abs/2204. 09888
-
Esser, P., Chennuru Vankadara, L., Ghoshdastidar, D.: Learning theory can (sometimes) explain generalisation in graph neural networks. Advances in Neural Information Processing Systems 34, 27043–27056 (2021)
-
Gilmer, J., Schoenholz, S.S., Riley, P.F., Vinyals, O., Dahl, G.E.: Neural message passing for quantum chemistry (2017)
-
Grimova, N., Macas, M., Gerla, V.: Addressing the cold start problem in active learning approach used for semi-automated sleep stages classification. In: 2018 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). pp. 2249–2253. IEEE (2018)
-
Hamilton, W.L.: Graph representation learning. Synthesis Lectures on Artifical Intelligence and Machine Learning 14(3), 1–159 (2020)
-
Hamilton, W.L., Ying, R., Leskovec, J.: Inductive representation learning on large graphs (2018)
-
Hochbaum, D.S.: Approximating covering and packing problems: set cover, vertex cover, independent set, and related problems. In: Approximation algorithms for NP-hard problems, pp. 94–143 (1996)
-
Hu, S., Xiong, Z., Qu, M., Yuan, X., Côté, M.A., Liu, Z., Tang, J.: Graph policy network for transferable active learning on graphs. Advances in Neural Information Processing Systems 33, 10174–10185 (2020)
-
Hu, W., Fey, M., Zitnik, M., Dong, Y., Ren, H., Liu, B., Catasta, M., Leskovec, J.: Open graph benchmark: Datasets for machine learning on graphs. arXiv preprint arXiv:2005.00687 (2020)
-
Kipf, T.N., Welling, M.: Semi-supervised classification with graph convolutional networks (2017)
18. Lao, D., Yang, X., Wu, Q., Yan, J.: Variational inference for training graph neural networks in low-data regime through joint structure-label estimation. In: Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. pp. 824–834 (2022)
19. Leman, A., Weisfeiler, B.: A reduction of a graph to a canonical form and an algebra arising during this reduction. Nauchno-Technicheskaya Informatsiya 2(9), 12–16 (1968)
20. Li, P., Wang, Y., Wang, H., Leskovec, J.: Distance encoding: Design provably more powerful neural networks for graph representation learning (2020)
21. Li, Q., Han, Z., Wu, X.M.: Deeper insights into graph convolutional networks for semi-supervised learning. In: Thirty-Second AAAI conference on artificial intelligence (2018)
22. Li, Y., Yu, R., Shahabi, C., Liu, Y.: Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. arXiv preprint arXiv:1707.01926 (2017)
23. Liao, R., Urtasun, R., Zemel, R.: A {pac}-bayesian approach to generalization bounds for graph neural networks. In: International Conference on Learning Representations (2021), https://openreview.net/forum?id=TR-Nj6nFx42
24. Lu, C., Krishna, R., Bernstein, M., Fei-Fei, L.: Visual relationship detection with language priors (2016)
25. Ma, J., Deng, J., Mei, Q.: Subgroup generalization and fairness of graph neural networks. arXiv preprint arXiv:2106.15535 (2021)
26. Ma, J., Ma, Z., Chai, J., Mei, Q.: Partition-based active learning for graph neural networks. arXiv preprint arXiv:2201.09391 (2022)
27. Milgram, S.: The small world problem. Psychology today 2(1), 60–67 (1967)
28. Morris, C., Ritzert, M., Fey, M., Hamilton, W.L., Lenssen, J.E., Rattan, G., Grohe, M.: Weisfeiler and leman go neural: Higher-order graph neural networks (2020)
29. Nishad, S., Agarwal, S., Bhattacharya, A., Ranu, S.: Graphreach: Position-aware graph neural network using reachability estimations (2021)
30. Oono, K., Suzuki, T.: Graph neural networks exponentially lose expressive power for node classification. arXiv preprint arXiv:1905.10947 (2019)
31. Ren, P., Xiao, Y., Chang, X., Huang, P.Y., Li, Z., Chen, X., Wang, X.: A survey of deep active learning (2020)
32. Ren, P., Xiao, Y., Chang, X., Huang, P.Y., Li, Z., Gupta, B.B., Chen, X., Wang, X.: A survey of deep active learning. ACM computing surveys (CSUR) 54(9), 1–40 (2021)
33. Sato, R.: A survey on the expressive power of graph neural networks. arXiv preprint arXiv:2003.04078 (2020)
34. Scarselli, F., Tsoi, A.C., Hagenbuchner, M.: The vapnik–chervonenkis dimension of graph and recursive neural networks. Neural Networks 108, 248–259 (2018)
35. Sen, P., Namata, G., Bilgic, M., Getoor, L., Galligher, B., Eliassi-Rad, T.: Collective classification in network data. AI magazine 29(3), 93–93 (2008)
36. Sinha, A., Shen, Z., Song, Y., Ma, H., Eide, D., Hsu, B.J., Wang, K.: An overview of microsoft academic service (mas) and applications. In: Proceedings of the 24th international conference on world wide web. pp. 243–246 (2015)
37. Tsubaki, M., Tomii, K., Sese, J.: Compound–protein interaction prediction with end-to-end learning of neural networks for graphs and sequences. Bioinformatics 35(2), 309–318 (2019)
38. Veličković, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., Bengio, Y.: Graph attention networks. arXiv preprint arXiv:1710.10903 (2017)
39. Verma, S., Zhang, Z.L.: Stability and generalization of graph convolutional neural networks (2019)
40. Wang, M., Zheng, D., Ye, Z., Gan, Q., Li, M., Song, X., Zhou, J., Ma, C., Yu, L., Gai, Y., et al.: Deep graph library: A graph-centric, highly-performant package for graph neural networks. arXiv preprint arXiv:1909.01315 (2019)
41. Wu, Q., Zhang, H., Yan, J., Wipf, D.: Handling distribution shifts on graphs: An invariance perspective (2022)
42. Wu, Y., Xu, Y., Singh, A., Yang, Y., Dubrawski, A.: Active learning for graph neural networks via node feature propagation. arXiv preprint arXiv:1910.07567 (2019)
43. Xu, D., Zhu, Y., Choy, C.B., Fei-Fei, L.: Scene graph generation by iterative message passing (2017)
44. Xu, K., Hu, W., Leskovec, J., Jegelka, S.: How powerful are graph neural networks? arXiv preprint arXiv:1810.00826 (2018)
45. Yang, C., Wu, Q., Wang, J., Yan, J.: Graph neural networks are inherently good generalizers: Insights by bridging gnns and mlps. arXiv preprint arXiv:2212.09034 (2022)
46. Yang, J., Ang, Y.Z., Guo, Z., Zhou, K., Zhang, W., Liu, Z.: Panoptic scene graph generation (2022)
47. Yang, Z., Cohen, W.W., Salakhutdinov, R.: Revisiting semi-supervised learning with graph embeddings (2016). https://doi.org/10.48550/ARXIV.1603.08861, https://arxiv.org/abs/1603.08861
48. You, J., Ying, R., Leskovec, J.: Position-aware graph neural networks (2019)
49. Zellers, R., Yatskar, M., Thomson, S., Choi, Y.: Neural motifs: Scene graph parsing with global context (2018)
50. Zhou, K., Huang, X., Li, Y., Zha, D., Chen, R., Hu, X.: Towards deeper graph neural networks with differentiable group normalization (2020)
51. Zhu, G., Zhang, L., Jiang, Y., Dang, Y., Hou, H., Shen, P., Feng, M., Zhao, X., Miao, Q., Shah, S.A.A., Bennamoun, M.: Scene graph generation: A comprehensive survey (2022)
This paper is available on arxiv under CC BY 4.0 DEED license.