Authors:
(1) Diptarka Chakraborty, National University of Singapore, Singapore
(2) Sourav Chakraborty, Indian Statistical Institute, Kolkata;
(3) Gunjan Kumar, National University of Singapore, Singapore;
(4) Kuldeep S. Meel, University of Toronto, Toronto.
Table of Links
4 An Efficient One-Round Adaptive Algorithm and 4.1 High-Level Overview
6 Acknowledgements and References
B An O(log log n)-query fully adaptive algorithm
2 Notations and Preliminaries

If the variation distance between two distributions is more than ε, then we say the distributions are ε-far (or just far, when it is clear from the context).
The Binomial distribution, with parameters n ∈ Z + and p ∈ [0, 1] denoted by Bin(n, p) is the distribution of the number of successes in n independent experiments, where each experiment yields a Boolean outcome, with success occurring with probability p and failure with probability 1 − p.
Definition 2.1 (COND Query Model). A conditional sampling oracle for a distribution D is defined as follows: the oracle takes as input a subset S ⊆ [n] and returns an element j ∈ S, such that the probability that j ∈ S is returned is equal to D(j)/D(S) if D(S) > 0 and 1/|S| if D(S) = 0. We denote such a conditional query by CONDD(S).
The formal definition of a k-round adaptive tester is given in [CG18]. For completeness, we present the formal definition of a one-round adaptive tester for equivalence in the COND Query Model.
Definition 2.2. Given conditional query access to distributions P and Q (over domain [n]), and given tolerance parameter ε as inputs, a one-round adaptive tester A makes conditional queries to the distributions in two rounds:

In our proof, we will extensively use concentration lemmas. In particular, we will use the following version of Chernoff bound.
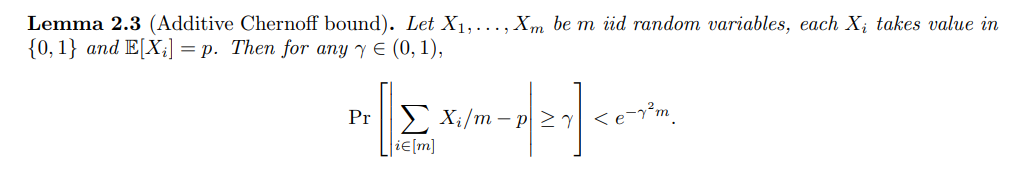
This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.

