Authors:
(1) Haleh Hayati, Department of Mechanical Engineering, Dynamics and Control Group, Eindhoven University of Technology, The Netherlands;
(2) Nathan van de Wouw, Department of Mechanical Engineering, Dynamics and Control Group, Eindhoven University of Technology, The Netherlands;
(3) Carlos Murguia, Department of Mechanical Engineering, Dynamics and Control Group, Eindhoven University of Technology, The Netherlands, and with the School of Electrical Engineering and Robotics, Queensland University of Technology, Brisbane, Australia.
Table of Links
General Guidelines for Implementation
VI. CASE STUDIES
In this section, we show the performance of the immersion-based coding algorithm on two use cases – privacy in optimization/learning algorithms and privacy in a nonlinear networked control system.
A. Immersion-based Coding for Privacy in Optimization/Learning algorithms
Machine learning (ML) has been successfully used in a wide variety of applications for multiple fields and industries. However, gathering extensive amounts of training data poses a challenge for ML systems. Commonly, increased data leads to improved ML model performance, necessitating the need for large datasets often sourced from various origins. Nonetheless, the process of gathering and using such data, along with developing ML models, presents significant privacy risks due to the potential exposure of private information.
In recent years, various privacy-preserving schemes have been implemented to address the privacy leakage in ML. Most of them rely on cryptography-based techniques such as Secure Multiparty Computation (SMC) [40] and Homomorphic Encryption (HE) [41], and perturbation-based techniques such as Differential Privacy (DP) [42]. Although current solutions improve privacy of ML algorithms, they often do this at the expense of model performance and system efficiency.
In this paper, we propose a privacy-preserving machine learning framework through the immersion-based coding algorithm. The main idea is to treat the optimization algorithm employed in the standard ML process as a dynamical system that we seek to immerse into a higher-dimensional system. We have explored the use of preliminary version of the ideas on this paper for privacy in federated learning with Stochastic Gradient Descent (SGD) as the optimization algorithm [26]. In this work, we generalize these results and implement immersion-based coding to encode all types of gradient descent optimization algorithms and employ the encoded optimizers to train machine-learning models.

Stochastic Gradient Descent (SGD) is one of the most common gradient descent optimization techniques in machine learning [43]. For SGD, function p(·, ·) can be written as follows:

2) Immersion-based Coding for Privacy-Preserving Gradient Descent Optimizers: In this section, we encode the gradient descent optimization algorithm given in (38), following the same technique that we discussed in Corollary 1, which is the immersion-based coding for remote dynamical algorithms with different time scales. The encoded optimization algorithm can be employed to provide privacy for the database and model in machine learning algorithms.
In this application, the optimizer in (38) is the original dynamical system Σ in (19) that we want to immerse to provide privacy. We consider a setting where the user who owns the database uploads the complete database D to the cloud, where the training process is executed by running the gradient-based optimizer (38). The optimizer iterates T times in the cloud to converge to a local optimum. Subsequently, the optimal model parameters vector w ∗ is sent back to the user. Since the user and cloud send the database and optimal model, which play the role of input and utility of the algorithm, only once, the number of user iterations is K = 1, and the number of local iterations is T. Functions f(·) and g(·) in (19) can be modeled as wt+1 = f(wt, D) := wt − p(wt, D) and w ∗ = g(wT ) := wT in this case. The model parameters wt, database D, and the optimal model parameters vector w ∗ can be considered as the internal variables ζt, input y, and utility u of the original algorithm Σ in (19).

The immersion and utility encoding maps are given by:
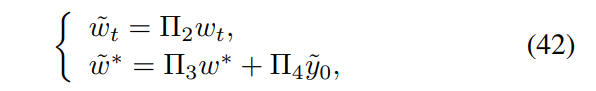
the target gradient descent optimizer is given by:
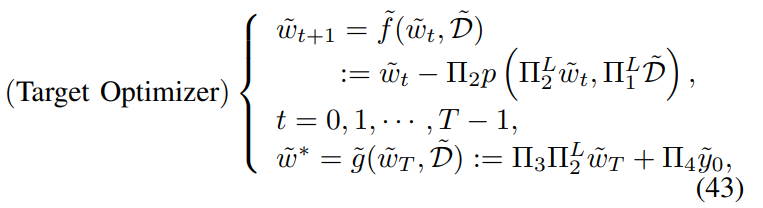
and the inverse function:
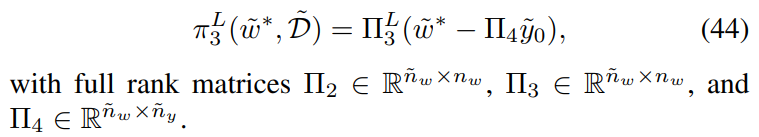
This approach can be employed to encode all kinds of gradient descent optimization algorithms that are typically used by machine learning algorithms. We will refer to machine learning algorithms that utilize immersion-based coding to preserve privacy as System Immersion-based Machine Learning (SIML).

3) Case Study of Optimization/Learning algorithms: In this section, we implement our proposed SIML scheme for performance evaluation using a multi-layer perception (MLP) [44] and a real-world machine learning database. Our investigation involves utilizing two optimization tools, i.e., Adam and SGD, on the MNIST database [45]. The experimental details are described as follows:
• Dataset: We test our algorithm on the standard MNIST database for handwritten digit recognition, containing 60000 training and 10000 testing instances of 28× 28 size gray-level images, which are flattened to the vectors of dimension 784.
• Model: The MLP model is a feed-forward deep neural network with ReLU units and a softmax layer of 10 classes (corresponding to the ten digits) with two hidden layers containing 256 hidden units and cross-entropy loss. The MLP model contains 269,322 parameters.
• Optimization tools: As optimization algorithms, the SGD and Adam optimizers with learning rate 0.001 and T = 50 epochs are employed to train ML models.
Our implementation uses Keras with a Tensorflow backend.

First, in Fig. 2, we show the impact of the proposed coding mechanisms by comparing one sample of the original MNIST dataset and its encoded format. As can be seen in this figure, the encoded image closely resembles the random term in the distorting mechanism, differing significantly from the original image. Therefore, adversaries can not infer any information from the original image by accessing the encoded one.
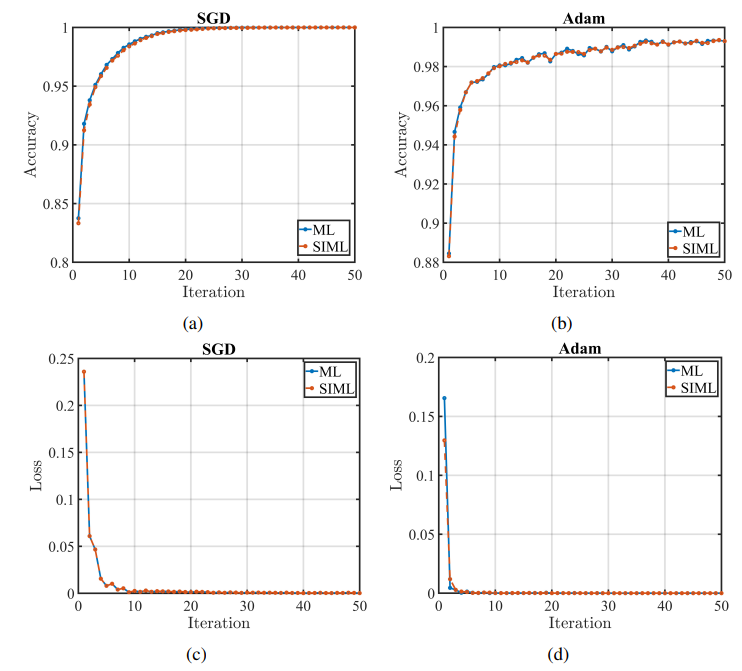
Then, the comparison between training accuracy and loss outcomes of the SIML and standard ML frameworks is illustrated in Fig. 3. In our implementation, the SIML framework utilizes target SGD and target Adam optimizers with the distorted MNIST database, while the traditional ML framework employs original SGD and Adam optimizers with the original MNIST dataset. It’s evident that the accuracy and loss metrics under the SIML configuration are similar to those in the non-privacy setting, indicating that SIML can incorporate cryptographic methods into ML systems without compromising model accuracy and convergence rate.
B. Privacy-aware Networked Control
We illustrate the performance of the immersion-based coding for networked control systems through a case study of a two-stage chemical reactor with delayed recycle streams. The authors in [46] propose an adaptive output feedback controller for this chemical reactor dynamics. We assume the controller is run in the cloud and aim to run it in a private manner using the proposed coding scheme. Consider the dynamic model of the reactor (as reported in [46]):

We use the following adaptive output feedback controller (see [46] for details) in order to achieve global adaptive stabilization of system (45):
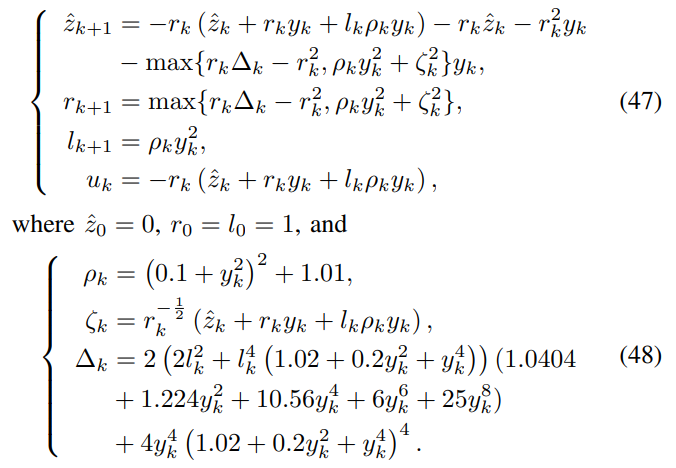
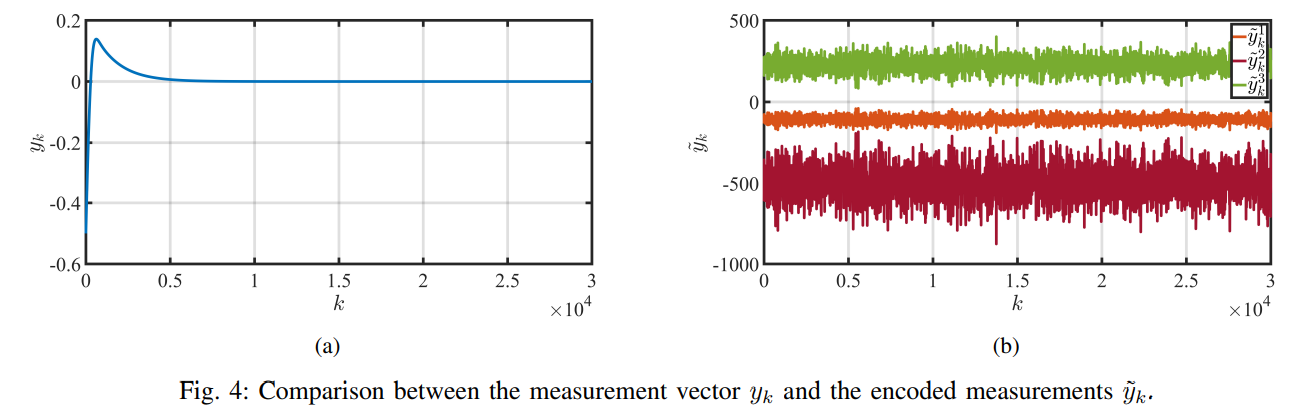
We consider the setting where the controller (47), (48) is run in the cloud. We employ the proposed immersion-based coding in Proposition 1 to enable a secure networked control system. The controller (47) can be reformulated in a compact form as follows.

The encoding and immersion maps are given by:
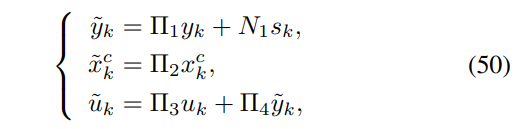
the target controller is given by:
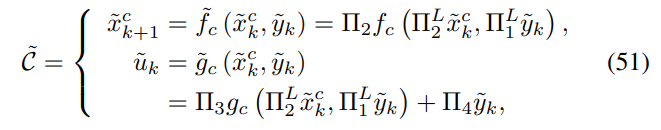
and the inverse function:


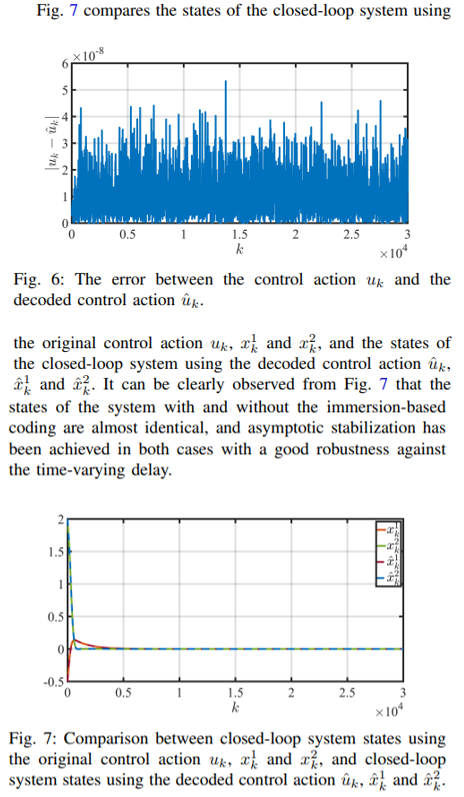
This paper is available on arxiv under CC BY 4.0 DEED license.

