Boosting Fairness and Robustness in Over-the-Air Federated Learning: Numerical Example

27 Oct 2024

Authors:

(1) Halil Yigit Oksuz, Control Systems Group at Technische Universitat Berlin, Germany and Exzellenzcluster Science of Intelligence, Technische Universitat Berlin, Marchstr. 23, 10587, Berlin, Germany;

(2) Fabio Molinari, Control Systems Group at Technische Universitat Berlin, Germany;

(3) Henning Sprekeler, Exzellenzcluster Science of Intelligence, Technische Universit¨at Berlin, Marchstr. 23, 10587, Berlin, Germany and Modelling Cognitive Processes Group at Technische Universit¨at Berlin, Germany;

(4) Jorg Raisch, Control Systems Group at Technische Universitat Berlin, Germany and Exzellenzcluster Science of Intelligence, Technische Universitat Berlin, Marchstr. 23, 10587, Berlin, Germany.

Table of Links

Abstract and Introduction

Problem Setup

Federated fair over-the-air learning (FedAir) Algorithm

Convergence Properties

Numerical Example

Conclusion and References

V. NUMERICAL EXAMPLE

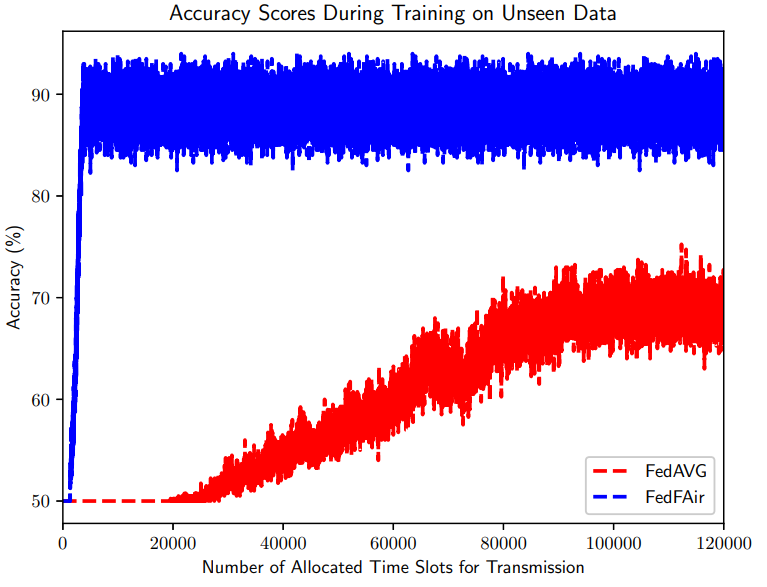
Fig. 1. Comparison of the performances FedFAir and FedAVG algorithms on unseen data during training in terms of their accuracy.

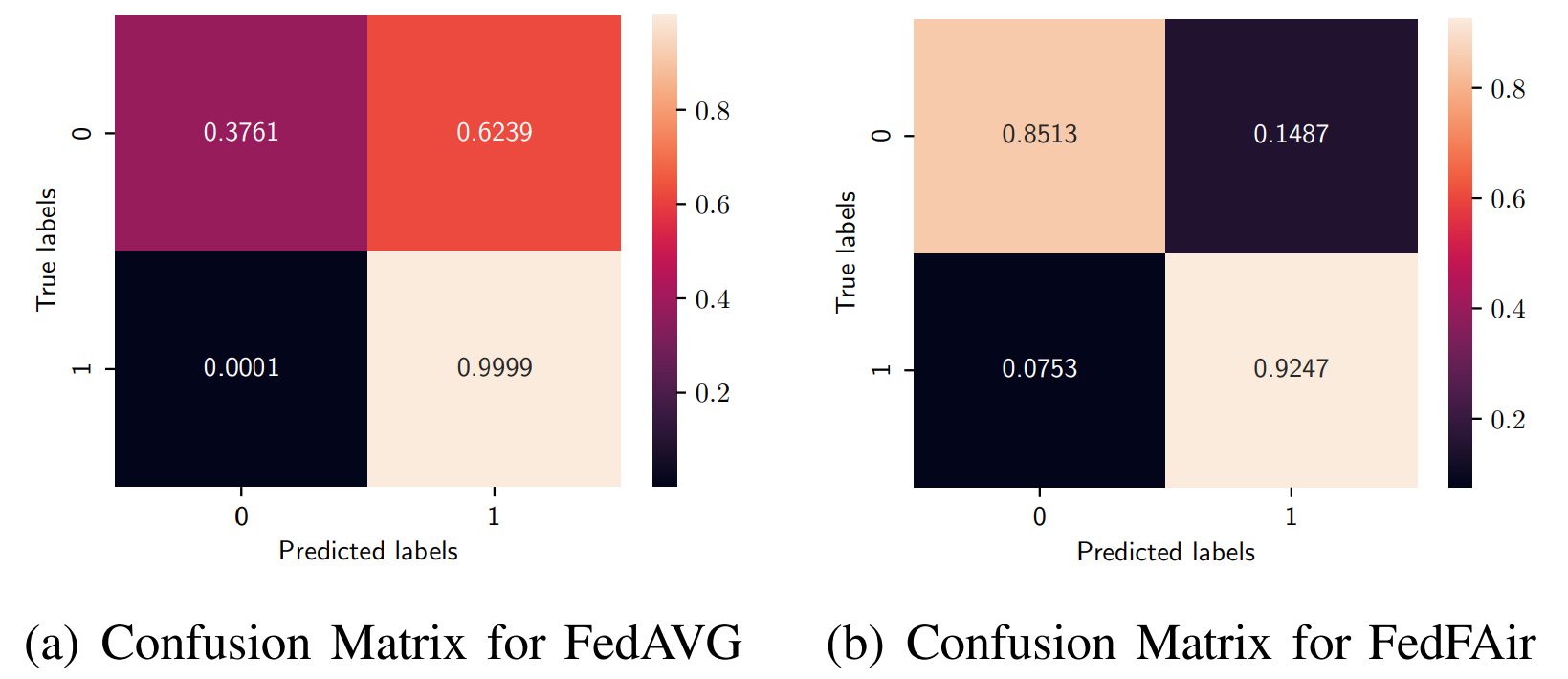
Notice that the FedAVG algorithm achieves approximately 70 − 75% of classification accuracy after 100000 iterations as it can also be seen in Fig. 1. However, due to the heterogeneity in distribution of the data, we observe that the FedAVG algorithm cannot properly identify the samples of data with labels 0. This can be seen from the confusion matrices in Fig. 2, where the FedAVG model cannot successfully recognize the data labeled as 0, whereas the FedFAir algorithm performs much better by recognizing a large percentage of data, both labelled 0 and 1.

nd 1. Additionally, we compare the FedFAir algorithm and the standard FedAVG [1] algorithm in terms of communication efficiency. For the latter, the TDMA scheme is used for communication between agents and the central unit. In this case, individual time slots are allocated for each agent to transmit its parameter vector at each communication round. After receiving parameter vectors, the central unit computes the average of them and sends it back to the agents. Since we consider a system with N = 12 agents, it takes N = 12 time slots per communication round for each agent to transmit its updated parameter vector while only 3 are needed for the FedFAir algorithm (see (13)), independent of the value of N. This makes the execution of one iteration of the FedFAir algorithm N/3 = 4 times faster than the execution of an iteration of the FedAVG algorithm.

Fig. 2. Comparison of Confusion Matrices

This paper is available on arxiv under CC BY 4.0 DEED license.