Authors:
(1) Diptarka Chakraborty, National University of Singapore, Singapore
(2) Sourav Chakraborty, Indian Statistical Institute, Kolkata;
(3) Gunjan Kumar, National University of Singapore, Singapore;
(4) Kuldeep S. Meel, University of Toronto, Toronto.
Table of Links
4 An Efficient One-Round Adaptive Algorithm and 4.1 High-Level Overview
6 Acknowledgements and References
B An O(log log n)-query fully adaptive algorithm
A MISSING PROOFS

Therefore, by additive Chernoff bound (Lemma 2.3), the value et = EstTail(D, i, S, β, b, m) returned by the algorithm satisfies
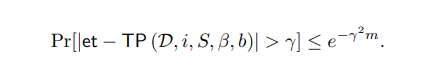
To prove Claims 4.10, 4.11 and 4.12, we will use the following concentration inequality that directly follows from Bernstein’s concentration inequality.






This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.

